Overview of Research
Chris Cox

Mathematical billiards, in which particles move freely until colliding with a boundary and then rebound according to the specular collision law angle in equals angle out, have long been studied as a model for physical systems, as a versatile tool for understanding dynamical systems more generally, and for the intrinsically interesting questions that arise, including some which are simple to pose but have long remained open. In recent decades, as new ideas have opened doors to understanding standard specular billiards more clearly, interest has grown in natural alternatives to the specular collisions model. Of particular interest to me are no-slip billiards, in which the bodies exhibit a nondissipative friction resulting in the exchange of linear and angular momentum at collisions, and related nonholonomic billiards and rolling systems.

The "no-slip strip", showing how a particle will remain bounded in an infinite corridor undergoing no-slip collisions.

Active Projects

Rolling systems and nonholonomic billiards

A sphere rolling on a surface (or other manifold, like the ray to the right) without sliding is an example of a nonholonomic system. While no-slip billiards are modeled without any explicit nonholonomic constraints, in Differential geometry of rigid bodies collisions and non-standard billiards (with Renato Feres ) we show that (at least in spirit) there is a certain affinity, as the natural physical assumptions on the collision map will ensure that it restricts to the identity on a certain non-slipping subspace. This idea was made more concrete in Rolling and no-slip bouncing in cylinders, with Feres, Scott Cook, and Tim Chumley, in which we show that small no-slip collisions very closely approximate the nonholonomic motion of a sphere rolling in a cylinder under an external force. Independently, Borisov, Kilin, and Mamaev partially bridged the no-slip/nonholonomic gap from the other side, showing that the two dimensional no-slip strip and ellipse emerge as limits of rolling systems respectively in an infinite cylinder and an ellipsoid. In Rolling systems and their billiard limits with Feres and Bowei Zhao, we extend this connection, showing that no-slip limits arise very generally as the small radius limit of nonholonomic rolling systems. Currently, we are interested in the dynamics of rolling systems; in particular, which distinctive features of no-slip billiards persist for positive radius rolling systems?

You can play around with some examples here.

The no-slip Galton board

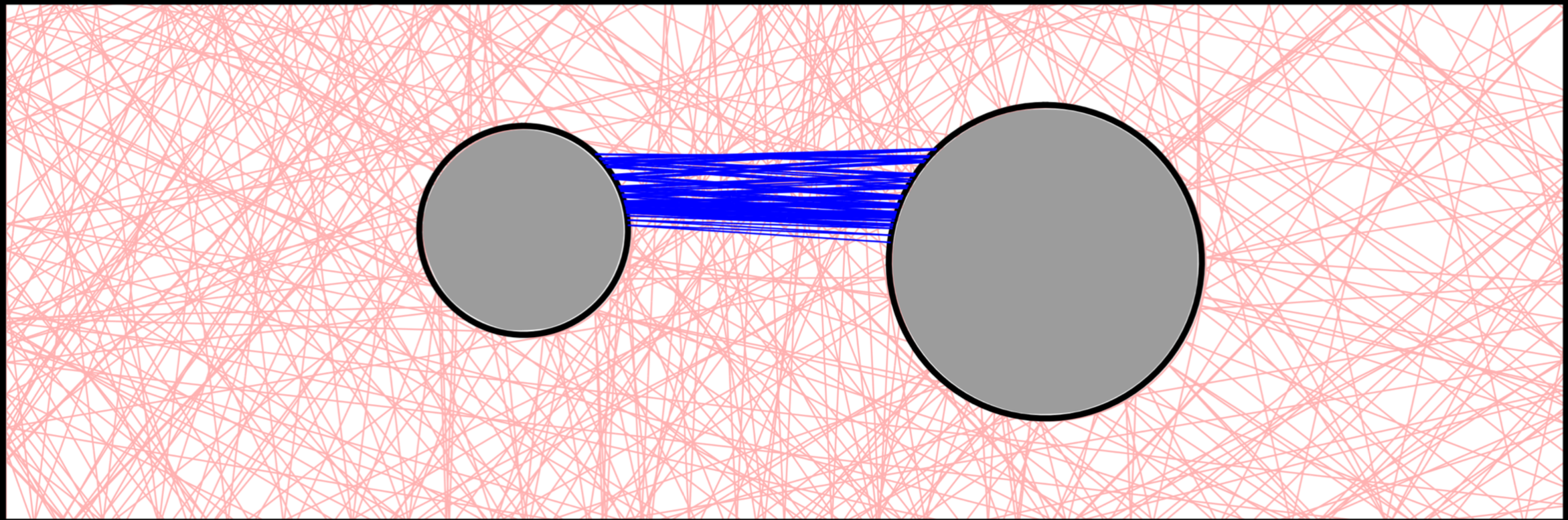
Lorentz gases, modeled by billiard systems with an array of scatterers, were introduced as a model for ions moving in a metal over a hundred years ago, and the broadly applicable model is still actively studied. The ideal Galton Board, essentially a Lorentz gas with an external force, modeling a bean machine in which particles fall dispersed by scatterers, is also of mathematical interest. Neither of these models has been previously considered in the context of the no-slip collision model; indeed, as invariant regions preclude the ergodicity of standard Sinai billiard (see blue trajectories, left) analytic study becomes difficult. However, many questions can still be broached numerically, and in the Summer of 2019 Scott Cook and I led a team of undergraduates working at Tarleton State University developing python code to run simulations of no-slip billiards under an external force. Working with Tim Chumley, we are currently preparing the results from these experiments.

Recent Projects

Dynamics of no-slip billiards

In my dissertation and in No-slip billiards in dimension two with Renato Feres, we begin to analyze the dynamics of billiards using the no-slip collision model. One characteristic of polygonal no-slip billiards, as seen for the phase portrait projection of the pentagon to the left, is the ubiquity of periodic point centering invariant regions, a generalization of the elliptic islands of standard ergodic billiards. These preclude ergodicity in polygons, as Feres and I showed with Hongkun Zhang at the University of Massachusetts Amherst, in Stability of periodic orbits in no-slip billiards.

Ergodic billiards

Standard specular billiards having boundaries formed by two arcs of circles may form flowers of two petals (if the internal angle is greater than pi), lemon billiards (if both edges bulge outward and meet at an angle less than pi), or moon billiards (if one side bulges in, forming a crescent moon shape). The first category are known to be ergodic by a criteria of Bunimovich. The latter two classes were studief by Hongkun Zhang and Maria Coriea (also of UMass Amherst). Hongkun and Maria let me work with them on a perturbation of these types known as umbrella billiards .

Past and Potential Student Research

Finding evidence of chaotic behavior in families of no-slip billiards

The question of whether any ergodic no-slip billiard exists is still an open question. In a Sinai type no-slip billiard, we may reduce the size of the apparent elliptic islands by decreasing the size of the scatterer (left). However, tiny elliptic islands seem to persist, as the one to the right, on a scale of around 0.5 percent of the full phase portrait to the left. Numeric techniques including calculating Lyapunov exponents, which give a measure of the chaotic tendencies, have not yet been used but should shed more light on the picture.

Persistently periodic no-slip billiards

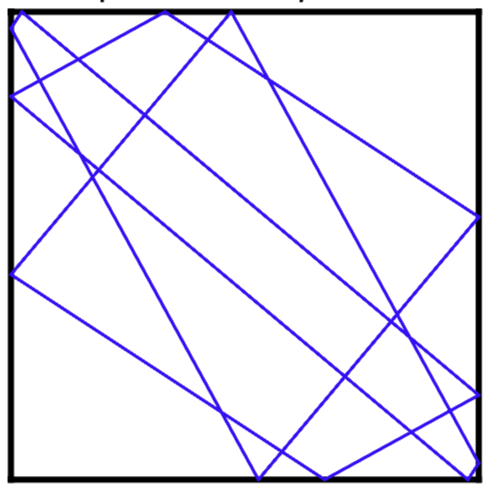Some no-slip wedges and and polygons display the curious property of persistent periodicity: no matter what the initial spin and velocity is, the orbit will be periodic. For example, for a no-slip equilateral triangle with uniform mass distribution particles, all orbits have period four or six. It is known that for uniform mass distribution, for any number n there is an angle such that the wedge has all (non-escaping) orbits periodic of period 2n. As of 2019, the equilateral triangle was the only known example for a closed polygon, but Tarleton graduate students Clayton Boone and Bishwas Ghimire independently found a mass distribution giving persistently periodic square (pictured) while in my modeling course. Bishwas continued working with me over the summer and used a numerical search algorithm to find a mass distribution giving a persistently periodic pentagon. There are a lot of open questions remaining and potential to continue this research.

Ergodicity of two arc specular billiards

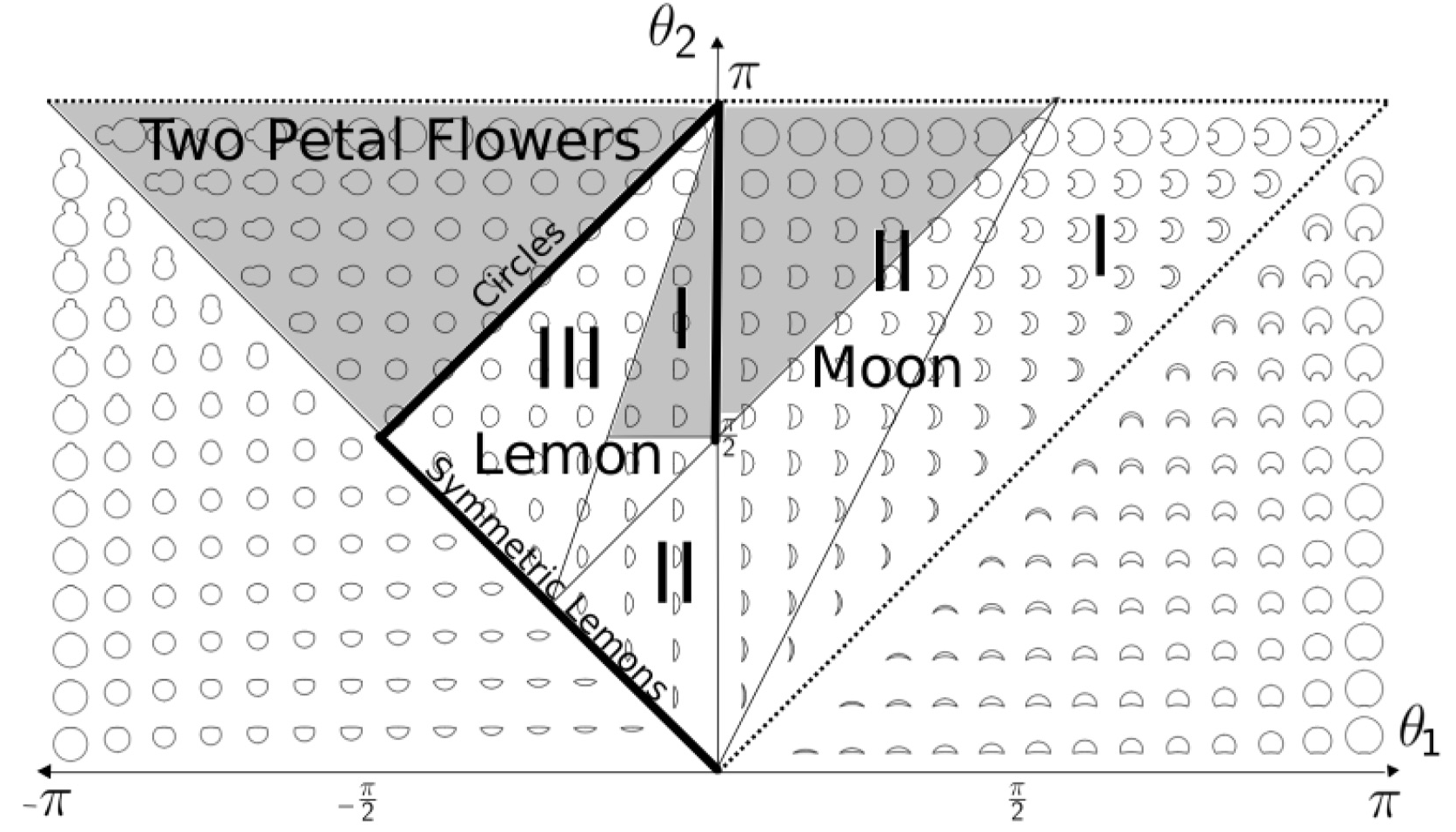
In my work with Zhang and Correia on umbrella billiards, as an extension on their work on moon and lemon billiards, we start to fill in a picture of the ergodicity of the complete family of two arc billiards (right). It would be nice to revisit this and give a much higher resolution of this picture. A key to doing so would be to automate numerical tests for ergodicity; implementing these seems quite feasible and a worthwhile pursuit more generally, beyond merely the investigation of two arc billiards.

Older Research

Soap bubble geometry

One of my first assignments as an undergraduate summer research student was to help edit a paper which our group leader Joel Foisy had worked on the previous summer, in which they show that the standard double bubble is the unique length minimizing enclosure of two regions in the plane. The next year the SMALL Geometry Group worked on the problem of the best enclosure of three regions, the triple bubble problem. One of the members of that group, Michael Hutchings , and our faculty advisor later proved the double bubble conjecture in R³, with Ritoré and Ros.

Steiner trees

The Steiner tree problem asks what is the minimal length network connecting a given set of points, possibly using additional internal vertices called Steiner points. Without additional assumptions, in a minimal network the edges will meet in threes at 120 degrees at Steiner points. My first foray into mathematical research was at the Williams College SMALL REU where we answered the question of whether more than three edges might meet at a Steiner points. (Short answer: yes! Longer answer: Networks minimizing length plus the number of Steiner points.) This work led me to an undergraduate thesis with Morgan on another variation of the Steiner problem, flow dependent networks , in which a flow is assigned between every pair of points and the unit length cost function for each edge depends on the flow through that edge.

Home